Рисуем фазовый портрет

24.03.2010 |

Для того, что бы «разглядеть» множество тех состояний, в которых побывал объект управления или в которые ему предстоит попасть, существует способ отображения динамики движения – так называемый «фазовый портрет».

Фазовый портрет материальной точки отображается на координатной плоскости в координатах ошибки и ее производной, как это показано на рисунке 10.

В общем случае, в качестве координат могут быть взяты и другие величины, взаимно-однозначно зависящие от координаты и скорости материальной точки, но указанное сочетание координат (говорят еще «базис») в контексте разработки системы управления наиболее удобен.

Те величины, которые однозначно определяют состояние объекта, называют координатами состояния или фазовыми координатами. В нашем случае это ошибка регулирования и ее производная. Таким образом, состояние объекта можно отразить в виде точки на координатной плоскости.

Многообразие всех принципиально возможных состояний объекта управления образуют фазовое пространство, в случае материальной точки – фазовую плоскость.

Множество всех состояний, через которых объект управления прошел или еще пройдет, называют фазовой траекторией.

На рисунке 10 представлены примеры фазовых траекторий материальной точки, которые соответствуют различным начальным состояниям. Крутизна фазовых траекторий зависит от соотношения массы материальной точки и действующей на нее силы.

Рисунок 10. Фазовый портрет.

Фазовые траектории, направленные вверх, описывают движение материальной точки под воздействием максимальной отрицательной силы. В этом случае, ускорение материальной точки отрицательное, поэтому производная ошибки растет в положительном направлении и все фазовые траектории направлены вверх.

Под воздействием положительной силы все фазовые траектории направлены вниз.

Пока производная ошибки отрицательная, ошибка изменяется в отрицательную сторону. Поэтому все фазовые траектории в нижней полуплоскости направлены влево. По аналогичной причине все фазовые траектории в верхней полуплоскости направлены вправо.

Любая фазовая траектория материальной точки подчиняется уравнению, следующему из уже известных вам законов движения материальной точки, приведенных к ошибке регулирования:

$\begin{matrix} \dot{e}(t)=\dot{e}_0-\frac{F}{m}t\\ e(t)=e_0+\dot{e}_0t-\frac{F}{m}\frac{t^2}{2} \end{matrix}$

Исключим время из первого уравнения:

$t=-\frac{m}{F}(\dot{e}-\dot{e}_0)$ .

Подставим во второе уравнение:

$e(t)=e_0+\dot{e}_0(-\frac{m}{F}(\dot{e}-\dot{e}_0))-\frac{F}{m}\frac{(-\frac{m}{F}(\dot{e}-\dot{e}_0))^2}{2}$

$e(t)=e_0+\frac{m}{F}(-\dot{e}_0\dot{e}+\dot{e}_0^{2}-\frac{1}{2}\dot{e}^{2}+\dot{e}_0\dot{e}-\frac{1}{2} \dot{e}_0^{2})$ .

Окончательно, получаем функцию ошибки от ее производной:

$e(t)=e_0+\frac{1}{2}\frac{m}{F}(\dot{e}_0^{2}-\dot{e}^{2})$ .

Эта функция позволяет построить фазовую траекторию материальной точки из любого начального состояния. Как это сделать, расскажу чуть позже, когда примемся за практические занятия. Кстати, установите себе MATLAB любой версии, где есть Symulink, скоро он нам понадобится.

Согласно выбранной ориентации системы координат фазового портрета, было бы более логично вывести зависимость производной от ошибки, но, к сожалению, это невозможно, будем пользоваться обратной функцией.

Вообще принятая ориентация фазового портрета принципиального значения не имеет – это просто дань привычки и первой книжке, в которой я про него прочитал. Но глаза привыкли к такой картинке, поэтому мне легче воспринимать и анализировать фазовый портрет именно в таком виде, а остальное – детали, не будем тратить на них свое время.

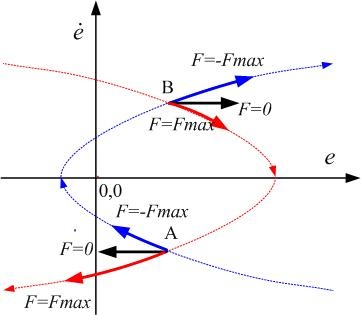
На рисунке 11 показано, как определятся движение материальной точки в фазовом пространстве. Из точки А, описывающей текущее состояние объекта управления, исходят множество фазовых траекторий, определяемых силой, воздействующей на материальную точку. В другом состоянии, обозначенном точкой В, картина аналогичная, только в зеркальном отражении.

Рисунок 11. Возможное движение материальной точки при разных действующих на нее силах.

Распечатайте эти рисунки и анализируйте их до тех пор, пока их содержание не станет для вас абсолютно ясным. Я позволю себе категорически настаивать на этом. Будет замечательно, если понимание фазового портрета отработается у вас на уровне рефлекса. И когда это произойдет, все последующие мои выкладки и рассуждения станут для вас просто самоочевидными. Наскоро набросав на листочке фазовый портрет, без лишних вычислений, вы с легкостью будете справляться с самыми сложными алгоритмами и заранее предугадывать поведение объекта управления.

Фазовый портрет – мощнейший инструмент для разработки систем управления и оценки их эффективности. Освойте его, и вы получите полную власть над вашим объектом управления.

«Ты должен управлять схемой, а не она тобой» – примерно так сказал мне лет этак 15 назад один очень жесткий преподаватель с кафедры САУ из «Политеха». Пусть это станет нашим девизом.

В следующей главе «разложим по полкам» релейный алгоритм управления. Вы увидите, как фазовый портрет просто и содержательно проиллюстрирует идею этого алгоритма.

Ликвидация ошибки и оптимальный закон торможения<< Оглавление >>В поисках идеала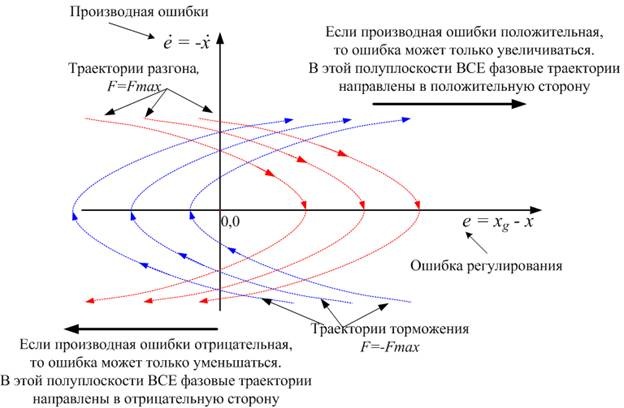

Рубрика: Новости

Progulschik:

13 июля 2011 в 21:05

Dobrogo vremeni sutok, uvazaemii administrator=) O4en davno hotel napusat Vam!!! tak kak Vi pishete dya studentov, to ,vozmozno, okazetsya poleznim skromnii sovet uchenika, kotorii vse osmislil po Vashemu saitu i po nemu ze proboval obyasnit’ odnogrupnikam, u kotorih bili voprosi. Na parah rebyata ne zadayut voprosov po tomu materialu chto ne ponyali, a potom sprashhivayut drug druga, poluchaya samie raznoobraznie po smislu otveti ot lyudei, kotorie v svoyu o4ered’ toze nichego ne ponyali’. Poluchaetsya vse dovolno pechalno, tak kak fiziku za vcem etim malo kto pitaetsya rassmotret’. V svyazu s etim predlagayu racshirit’ obyasnenie samogo bazovogo ponyatiya kursa, fazovogo portreta sistemi, tak kak v 90% neponimaniye skachet ot nego, a chto eto takoe prakticheski nikto iz rebyat tak u ne vzyalsya prochuvstvovat’ do konca ( operiruyut ponyatiem, ne ponimaya smisla)._____________________________Takim obrazom, sovetuyu vse ze napisat dannii razdel dlya dvornikov (daze ne dlya chainikov), dolzno ochen pomoch. A umenno: perenisti ili produblirovat’ primer s razborom fazovogo portreta telegi v dannii razdel do vivodov po razdelu; dobavitb fizicheskii smisl proizvodnoi ot oshibki(naprimer “e’ pokazivaet kak izmenyaetsya sila tyagu dvigatelya”) u oshibki (proshu ne smeyatsya, voprosi bili) i videlit’ vse zirnim. Dalee sleduet v primer dobavit grafiki odin pod drugim e(t), e'(t), v(t), x(t), a v razdele pro avtokolebaniya u skolzyaschii rezim opisatb za schet chego v tipovoi opisannoi Vami (kstati ochen udachno) telege zapasaetsya energiya u chto sistema inercionna (opyat’ fiziku u poprosxhe). Ya uveren, chto dannoe uproscheniye pozvolit ponyat material GORAZDO luchshe. _________p.s. Proshu prostit’ za angliiskuyu raskladku (drugoi klavi pod rukoi net) u za to, chto proshu silno uprostit’ opisaniye. S uvazeniyem, I.M.

Ответить

В поисках идеала. Эталон движения материальной точки.:

20 сентября 2013 в 18:37

[…] Рисуем фазовый портрет<< Оглавление >>Берем MATLAB за Simulink Рубрика: Новости […]

Элементарная теория автоматического управления

Рисуем фазовый портрет

Комментарии (2) на “Рисуем фазовый портрет”

Добавить комментарий для В поисках идеала. Эталон движения материальной точки.