Электропривод повышенной комфортности. Работа релейного управления в идеальных условиях.
Комфорт – (англ. comfort). Комплекс максимально благоприятных для субъекта условий внешней и внутренней среды, включающий и факторы психологические. В состоянии К. отмечается отсутствие напряжения психических и физиологических функций организма. В значительной мере чувство К. зависит от состояния гомеостаза. О субъективных ощущениях, присущих состоянию К., говорят как о чувстве К. (Определение из медицинского словаря).
Вот надо же, а я комфорт воспринимал совсем не так. Допустим, жесткий цейтнот в условиях, приближенных к «боевым»: с дымом и копотью, кипящим мозгом и плавящейся проводкой. Но, если, при всем, при этом, работа доставляет неимоверное удовольствие – комфорт это или нет? Вообще, скользкий термин, неопределенный. Вот, лично для меня, комфорт наступает тогда, когда я, собственной персоной, («О чудо!») на самом деле начинаю управлять своим замечательным изделием, а не наоборот. «Отсутствие напряжения психических и физиологических функций организма» – пожалуйста, будьте, как говорится, любезны – все по словарю, по определению.
А вообще интересно, как бы мы распорядились «максимально благоприятными для субъекта условиями внешней и внутренней среды». Попробуем представить, что на самом деле работаем в «тепличных условиях», идеальность которых нарушает только необходимость
перейти к академическому тону – все-таки серьезный дальше пойдет разговор, вы понимаете, о чем я.
Напомню, что в предыдущем разделе мы выяснили, что если пренебречь некоторыми особенностями электропривода нашей тележки, то все законы движения сводятся к материальной точке. А это уже для нас «проще – простого» – только надо сразу вспомнить что такое «оптимальная», «фазовая», «траектория».
Сразу скажу, что, в примере с тележкой оптимальная фазовая траектория подчиняется закону
Это легко доказать, так как крутящий момент двигателя пересчитывается к тяге привода, приложенной к центру масс. При максимальном управлении максимальная тяга привода будет описываться следующим выражением:
.
Приведенный момент инерции пересчитывается к эквивалентной массе:
.
А максимальное ускорение:
,
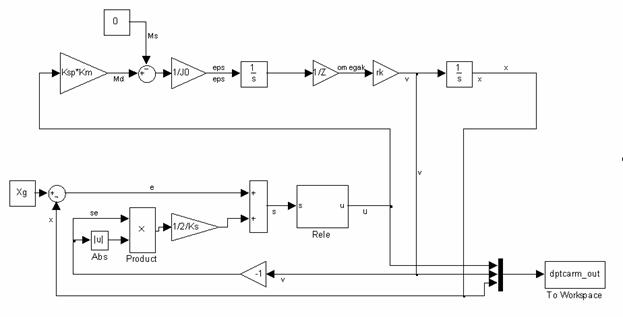
из чего, очевидно, и следует вид оптимальной фазовой траектории. На рисунке 1 представлена модель системы управления, разработанная в MATLAB Simulink.
В приложенных файлах представлена программа вычислений. Сразу признаюсь, реле пришлось немного доработать- численные методы с идеальным реле не справляются. И это совершенно понятно – в области, близкой к нулю ошибки коэффициент усиления системы управления становится практически бесконечным: на малые изменение координат она отвечает кардинальным изменением управления. Конечно же ни какому численному методу это не под силу. Впрочем главный момент – разгон -торможение модель отрабатывает идеально, как в теории. А вот после выхода к нулю ошибки и ее производной начинают проявлять себя нюансы численного моделирования. Вот я их и обошел, несколько своеобразным образом. Но на эталон движения это существенно не повлияло. Вообщем, пользуйтесь.
Архив с программой и модель: cardpt.
Моделирование проводилось при следующих параметрах.
%коэффициент силового преобразователя [А]
Ksp=7.5;
%Магнитный коэффициент [Нм/(рад А)]
Km=0.012;
%Момент инерции ротора двигателя [кг(м/рад)^2]
Jp = 1e-6;
%Радиус колеса [м]
rk=0.075;
%Масса колеса [кг]
mk=pi*(rk^2-(rk-0.01)^2)*0.02*1.2*1000;
%Момент инерции 4-х колес [кг(м/рад)^2]
Jk=0.8*mk*rk^2*4;
%Масса тележки без полезной нагрузки [кг]
m0=11;
%Расчетная масса груза [кг]
mn=5;
%Коэффициент редукции
Z = 60;
При полном соответствии модельных и расчетных параметров, моделирование показывает переходные процессы, оптимальные по точности и по быстродействию. Графики переходных процессов при разном заданном положении показаны на рисунках 2, 3 и 4. На рисунке 5 показан фазовый портрет. Неплохой такой портрет получился, качественный. Система управления работает как часы: разгон-торможение-полная остановка, и именно в той точке, где положено. Вот только весь восторг куда-то пропал, я бы даже сказал, скучновато получилось, обыденно. Вообще удивительное это дело: приедается комфорт, начинает тянуть на подвиги. Но это все не про нас: нам скучать некогда – электропривод полон сюрпризов; в скором времени вы в этом убедитесь.
Рисунок 1. Модель системы в MATLAB Simulink.
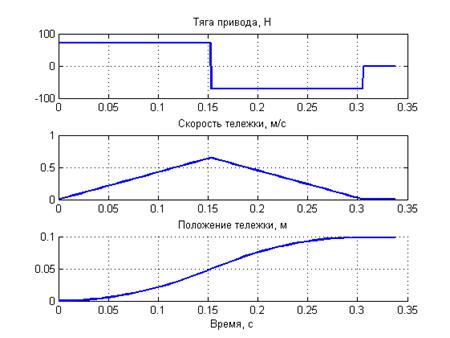
Рисунок 2. Оптимальные переходные процессы в приводе при заданном положении 0.1 м.
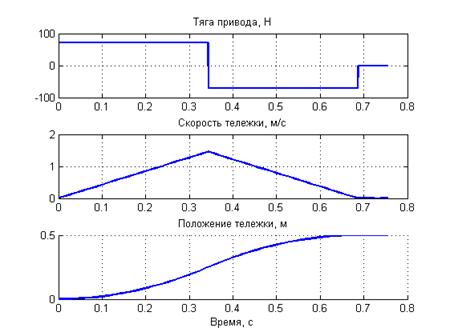
Рисунок 3. Оптимальные переходные процессы в приводе при заданном положении 0.5 м.
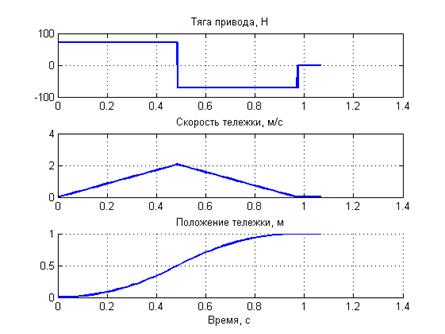
Рисунок 4. Оптимальные переходные процессы в приводе при заданном положении 1 м.
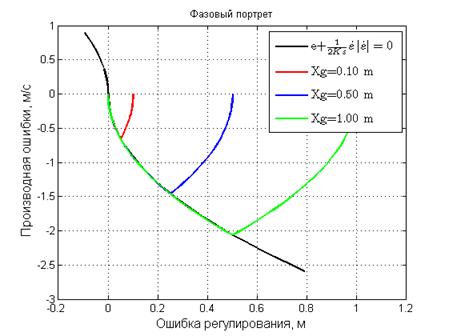
Рисунок 5. Фазовый портрет оптимальных переходных процессов.
Первые шаги в электропривод<< Оглавление >>Кибернетические качели
[...] [...]