Элементарная теория автоматического управления

Вот так это выглядит на практике

Он растёт, боясь мороза,

У папы с мамой на виду,

Как растение мимоза

В ботаническом саду.

Сергей Михалков

Я, признаюсь, вовсе забыл, к чему мне вдруг показался уместным в качестве эпиграфа использовать знакомое всем с детства четверостишье. Возможно, думал о том, что к комфорту на самом деле привыкаешь с большой легкостью. А уж как попадается чуть более сложное изделие, так сразу включается метод «научного тыка» и «выпуклого военно-морского глаза». То есть начинаешь бить по площадям. И даже время от времени попадаешь, что называется «в точку». Вот, каждый раз, в подобной ситуации, радость завершенной работы всегда омрачалась пониманием, что наука здесь оказалась снова не причем. За науку обидно и за себя – в следующий раз снова начинать сначала. Нет, это не кибернетика, а баловство, честное слово. Это не по нам. Поэтому пора начать разбираться, а что же на самом деле происходит, когда ваше изделие перестает соответствовать идеальной детерминированной и стационарной модели. Могу поспорить, некоторые из моих глубокоуважаемых читателей поморщились, встретив сразу два зубодробительных термина подряд. Ни чего, привыкайте, в книгах прямо так и пишут.

Детерминированность означает, что структура объекта управления и его параметры заранее известны.

Стационарность означает, что структура и параметры объекта управления остаются неизменными во времени.

В моем любимом примере с тележкой, вернее с материальной точкой, объект управления, собственно, таковым и является – детерминированным и стационарным. Поэтому управление материальной точкой до безобразия элементарно. Однако, что произойдет, если реальный объект управления начинает в некоторой степени отличаться от своей идеальной модели?

В той же самой управляемой тележке мы не можем за ранее определить приведенную массу, так как она зависит от массы груза. Но это полбеды – в конце концов, вполне возможно перестраивать алгоритм каждый раз, когда меняется полезная нагрузка. А вот что происходит, если меняется тяга двигателя? Она, как раз, может зависеть от чего угодно – от нагрузочной способности источника питания, от температуры двигателя и элементов трансмиссии, от качества и наклона дорожного полотна, etc.

Теперь, рассмотрим простой случай и допустим, что система управления была изначально рассчитана, точно так, как в предыдущем разделе, на некоторую приведенную массу.

Далее, нагрузим тележку так, что бы ее приведенная масса существенно увеличилась, например, в 2 раза. Что же мы увидим в результате? Тележка поведет себя так, как показано на рисунках 1,2 и 3. Там показаны переходные процессы сигнала управления, скорости и положения тележки при различных величинах заданного положения. Обратите внимание, что, независимо от заданного положения, тележка не останавливается в заданном положении, а некоторое время продолжает совершать колебательные движения в районе заданной точки, так как будто бы она к ней привязана пружиной.

Понять происходящее поможет фазовый портрет, представленный на рисунке 4. Там показана расчетная фазовая траектория, соответствующая расчетной полезной нагрузке сплошнаячернаялиния и реальная фазовая траектория штрихпунктирнаячернаялиния. Как показано на рисунке, реальная фазовая траектория проходит более полого, чем расчетная. Поэтому, система управления каждый раз, слишком поздно включает торможение. При этом тележка набирает чрезмерно много кинетической энергии, и на оставшемся пути привод не может совершить необходимую работу, что бы забрать всю накопленную энергию. Поэтому тележка постоянно «проскакивает» заданное положение.

Такой режим работы называется «автоколебательным». Назван он так, потому что система управления сама раскачивает тележку, без постороннего вмешательства. Это совершенно неприемлемый режим работы. Крайне неприятное впечатление вызывают эксперименты, когда та же тележка или манипулятор робота на полной скорости таранит стену или любое другое препятствие. Причем, эта неприятность далеко не единственная.

Например, любой механик подтвердит вам мои слова о том, что для остановки автоколебаний в механической системе требуется гораздо больше энергии, чем для их возбуждения. Кроме этого, в электромеханической системе всегда найдется такое сочетание неучтенных зазоров и упругостей, которое обязательно позаконуМуравызовет резонансные автоколебания, бороться с которыми исключительно трудно.

В роботе Пума неудачный выбор фазовой траектории приводит к еще большим неприятностям. На самом деле, представьте себе ситуацию, когда три достаточно мощных привода начинают с рычанием качать увесистые звенья манипулятора. В этот момент робот становится неуправляемым – силовые преобразователи отрабатывают что угодно, только не заданный ток, да и сигнал заданного тока тоже становиться абсолютно неадекватным – начинает сбоить электроника и измерительные устройства. Одним словом авария. С Пумой, конечно, такое безобразия мы не допускали, срабатывала встроенная аппаратная защита, но, еще раз повторюсь, впечатления крайне неприятные.

В домашних же условиях я намеренно и, что характерно, с легкостью повторял эту ситуацию, в результате чего неоднократно заменял комплект шестерен в редукторе – они рассыпались, не выдержав такого издевательства.

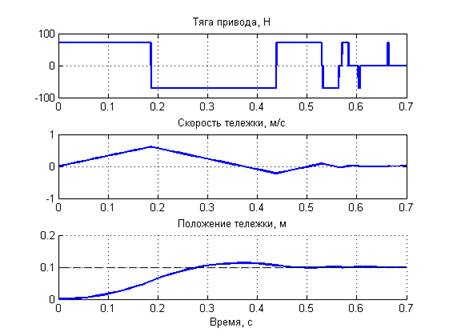
Рисунок 6. Автоколебательные переходные процессы при задании перемещения 0.1м.

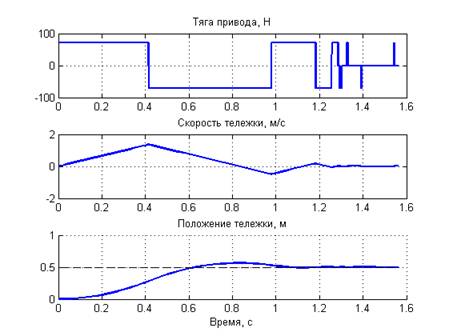
Рисунок 1. Автоколебательные переходные процессы при задании перемещения 0.5м.

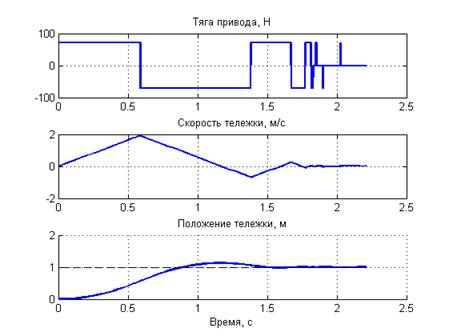
Рисунок 2. Автоколебательные переходные процессы при задании перемещения 1м.

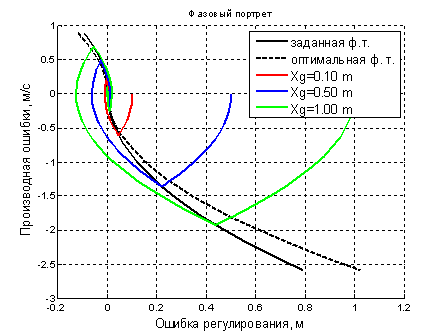
Рисунок 3. Автоколебательные переходные процессы при разном заданном перемещении.

Электропривод повышенной комфортности<< Оглавление>> Как ее убить

Комментарии (2) на “Кибернетические качели. Работа релейного регулятора в автоколебательном режиме.”