Пора брать быка за рога. Моделировать простые системы управления в MATLAB весьма просто и удобно.

Интернет учебник Matlab Simulink – И.В.Черных. “Simulink: Инструмент моделирования динамических систем

Далее приводится разработка системы управления положением тележки, которая рассматривается как материальная точка.

Для начала необходимо создать модель системы управления в Matlab Simulink. Например, такую модель, какая получилась у меня. Она показана на рисунке 1.

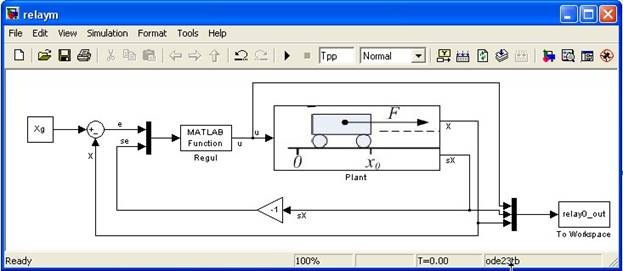
Рисунок 1. Модель системы управления в Matlab Simulink.

На схеме обозначено Regul – модель регулятора, Plant- модель объекта управления, «To Workspace»- блок, сохраняющий результаты моделирования в структуру relay0_out, доступную для обработки в исполняемых файлах MATLAB.

На следующих роликах показано с чего, собственно, начать.

Начало работы – организация рабочего места

 

Как написать простой скрипт на языке Matlab

 

Разработка модели объекта управления

 

Разработка модели системы управления

 

Постановка серии вычислительных экспериментов

 

Структура объекта управления представлена на рисунке 2. Все блоки объекта управления объединены в подсистему «Plant».

Представленная модель имитирует работу привода, состоящего из силового преобразователя, мотора и колеса. На вход объекта управления поступает сигнал управления. Этот сигнал умножается на максимальную силу тягупривода Fo. Таким образом, моделируется работа силового преобразователя и двигателя.

Далее, сила делится на массу тележки, получаем ее ускорение сигналssX. Интегрируем один раз, получаем скорость производнаякоординатытележки?сигналsX. После второго интегрирования получаем перемещение тележки координата?сигналX.

Выходными сигналами подсистемы являются сигналы координаты и ее производной.

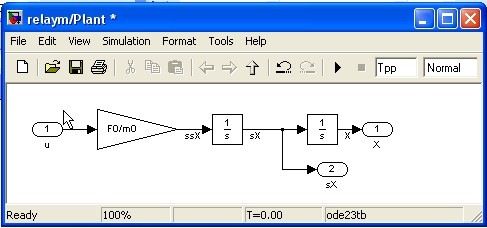
Рисунок 2. Модель объекта управления.

Как уже упоминалось ранее, в Simulink есть возможность объединять различные блоки в подсистемы. Как это сделать – смотрите на видео «Разработка модели объекта управления». При этом, возможно отображать подсистемы различными способами, что позволяет создать довольно качественное и интуитивно понятное оформление разрабатываемой системы. На рисунке 3 показан диалог настройки отображения подсистемы. В качестве примера там показано, как в блоке подсистемы отобразить картинку.

В диалог настройки отображения подсистемы можно попасть следующим образом – щелкаем на блок подсистемы правой кнопкой мыши, далее, если редактируете отображение подсистемы в первый раз, выбираем во всплывающем меню «Mask Subsystem…», в последующих случаях- «Edit Mask».

После того, как «маска» создана, для работы с содержимым подсистемы, в всплывающем окне выбираем команду «Look Under Mask».

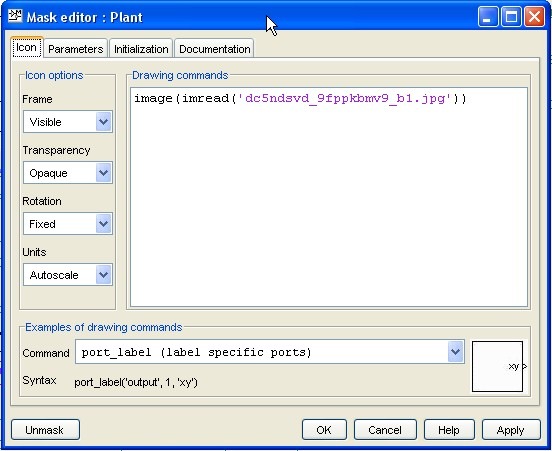
Рисунок 3. Настройка отображения подсистемы.

Отдельно стоит рассмотреть реализацию регулятора. Так как в рассматриваемых нами системах регулятор имеет довольно сложную структуру, то я предпочел реализовать работу регулятора в отдельной функции на языке Matlab. Текст этой функции представлен на Рисунке 5. Эта функция называется «relay_control0» и сохранена в файле с таким же названием: «relay_control0.m». Указанная функция получает четыре параметра – величина ошибки, ее производной, расчетные величины максимальной силы и массы.

В структуру системы управления функция «relay_control0» включается посредством блока «MATLAB Function», который находится в разделе «User-Defined Function» библиотеки блоков Simulink. Как правильно настроить этот блок, показано на рисунке 6.

Как показано на рисунке 1, на этот блок поступают сигналы, объединенные блоком «Mux» SignalRouting в один вектор. Внутри блока «MATLAB Function» компоненты этого вектора, согласно документированным договоренностям определяются через следующие обозначения: u1 и u2. Номер компоненты вектора u соответствует порядку включения сигнала в блок «Mux». Так, если сигнал ошибки поступает на «Mux» первым, а сигнал производной ошибки вторым, то в блоке «MATLAB Function» они будут соответственно обозначаться u1 и u2.

Таким образом, на каждом шаге моделирования, система расчета будет вызывать функцию «relay_control0» и подставлять в нее текущие значения ошибки и ее производной.

По моему личному мнению – это довольно удобный вариант реализации сложных структур. Впрочем, у меня есть сомнения по поводу некоторых возможностей Simulink, таких как линеаризация и оптимизация расчетов, которые наверняка становятся малоэффективными при таком исполнении модели. Впрочем, на данный момент это не играет особой роли. Кстати сказать, будет очень полезно, если вы сами поэкспериментируйте с разными вариантами реализации регулятора, и выясните какая модель и при каких условиях будет наиболее эффективной при расчетах. Я же в недалеком будущем планирую сам это проверить и доложить по форме.

Рисунок 5. Текст функции, моделирующей работу регулятора.

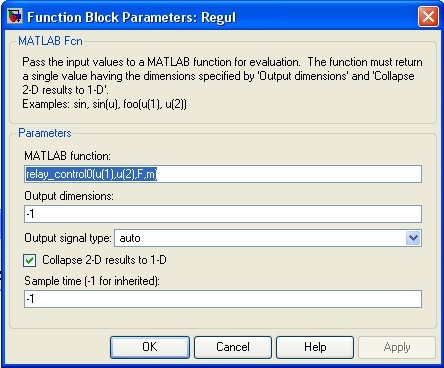
Рисунок 6. Настройка блока «MATLAB Function».

На рисунке 7 представлен пример настройки блока «To Workspace». Это блок позволяет сохранить результаты расчетов в виде структуры данных. Имя этой структуры задается в поле «Variable name». В нашем случае имя этой структуры- «relay0_out». Как ее правильно использовать показано в тексте программы, которая позволяет провести серию экспериментов и показать работу системы с релейным регулятором при разных заданных перемещениях.

Упомянутая программа производит следующие действия: инициализирует параметры объекта управления, определяет различные величины заданного перемещения, производит вычисления переходных процессов и отображает их на графиках, которые представлены на рисунках 8 – 11.

Обратите внимание на возможность MATLAB обеспечить очень приятное оформление графиков, в том числе возможность вывода различных символов в формате «LaTex»»

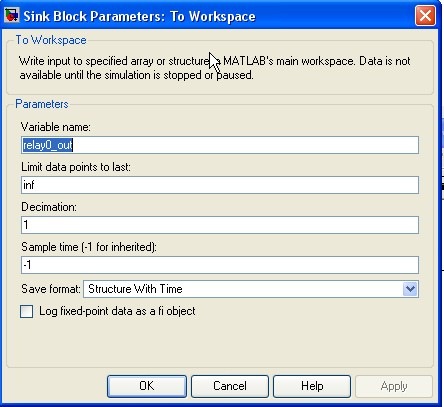
Рисунок 7. Настройки блока «To Workspace»

Далее приведен текст программы, который обеспечивает постановку нескольких вычислительных экспериментов и вывод результатов вычислений на нескольких графиках.

%=====================================================

% Готовимся к работе -  убираем с экрана все лишнее.

close all;

clear all;

% ПАРАМЕТРЫ ОБЪЕКТА УПРАВЛЕНИЯ

% Параметры  объекта управления разбиты на “реальные” и “расчетные”.

% Реальны параметры – это те, которыми объект управления обладает на “самом

% деле”. Их величины используются для моделирования поведения объекта

% управления.

% Расчетные параметры объекта управления – это предполагаемые нами оценки реальных параметров.

% На их основании проводится расчет регулятора. Поэтому они и называются “расчетными”.

 

F0=0.9;%Реальная максимальная тяга

m0=1;%Реальная масса

 

F=0.9;%Расчетная максимальная тяга

m=1;%Расчетная масса.

 

% ПАРАМЕТРЫ МОДЕЛИРОВАНИЯ

vXg=[0.1,0.5,1];%Заданная координата

N=lengthvXg; %количество проводимых экспериментов

colors={‘r’,’b’,’g’};

 

% ОПТИМАЛЬНАЯ ФАЗОВАЯ ТРАЕКТОРИЯ

%расчет оптимальной фазовой траектории

maxx=maxvXg

maxTpp=2*sqrtm0/F0?maxx;

maxsx=maxTpp*F0/m0/2*1.3;

%Задаем диапазон по оси ординат  производнаяошибки

vse=maxsx/3:-maxsx/20:-maxsx;

%Расчитываем фазовую траекторию ошибкарегулирования

ve=-m0/F0/2*vse.*absvse;

%рисуем оптимальную фазовую траекторию

figureN+1

setgcf,?Color?,?w?

plotve,vse,?k?,?LineWidth?,2

title ‘Фазовый портрет’

grid on

% Список строк для подписи графиков на фазовом портрете

lbl={‘e+m2Fe?|e?|=0′};

for i=2:N+1

lbl{i} = sprintf?Xg=);

end

%расчет переходных процессов

for i=1:N

%заданнок перемещение

Xg=vXgi;

%время переходного процесса

Tpp = 2*sqrtm/F?Xg*1.1;

%запускаем моделирование

sim?relaym.mdl?

%после расчета, структура relay0_out

%содержит результаты расчета

 

%время

t= relay0_out.time;

%сигнал управления

u=relay0_out.signals.values:,1;

%производная координаты скорость

sx=relay0_out.signals.values:,2;

%координата

x=relay0_out.signals.values:,3;

%отобразим результаты расчетов

figurei

setgcf,?Color?,?w?

subplot3,1,1

plott,u?F,?LineWidth?,2

title?Тягапривода,Н?

grid on

subplot3,1,2

plott,sx,?LineWidth?,2;

title?Скоростьтележки,м/с?

grid on

subplot3,1,3

hold on

plott,x,?LineWidth?,2;

plot[0,max(t],[Xg,Xg],’k–‘);

hold off

title?Положениетележки,м?

grid on

xlabel?Время,с?;

figureN+1

hold on

plotXg?x,?sx,colorsi,?LineWidth?,2

hold off

end;

figure N+1;

ylabel?Производнаяошибки,м/с?,?FontSize?,12

xlabel?Ошибкарегулирования,м?,?FontSize?,12

legendlbl,?FontSize?,12,?Interpreter?,?LaTex?

%=========================================

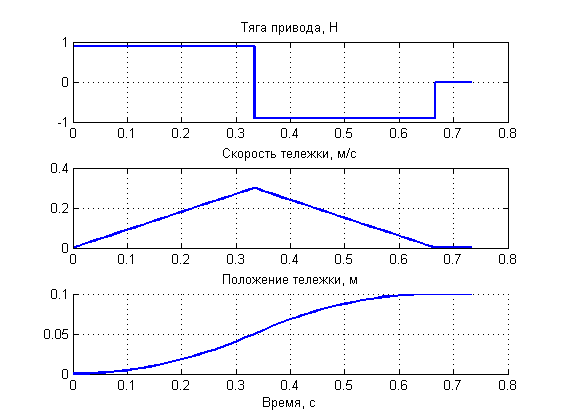
Рисунок 8. Работа системы управления при заданном перемещении 0.1 м.

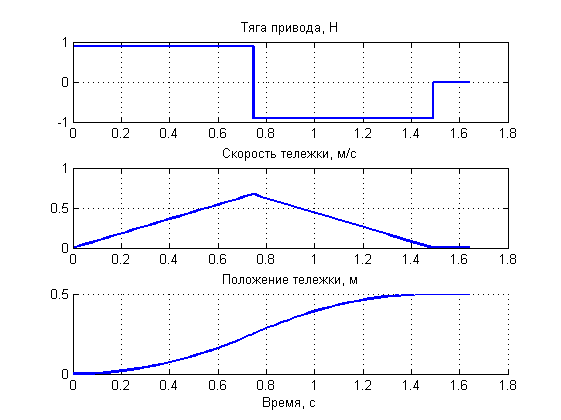
Рисунок 9. Работа системы управления при заданном перемещении 0.5 м.

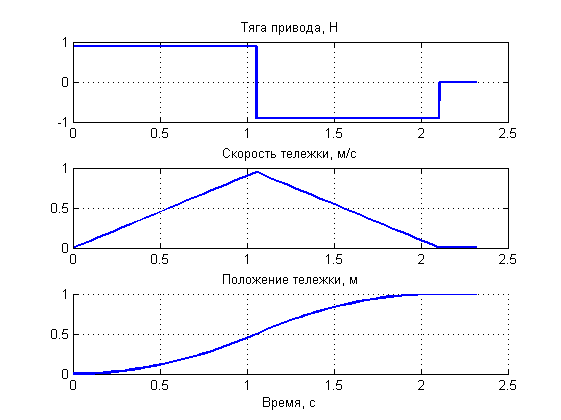
Рисунок 10. Работа системы управления при заданном перемещении 1 м.

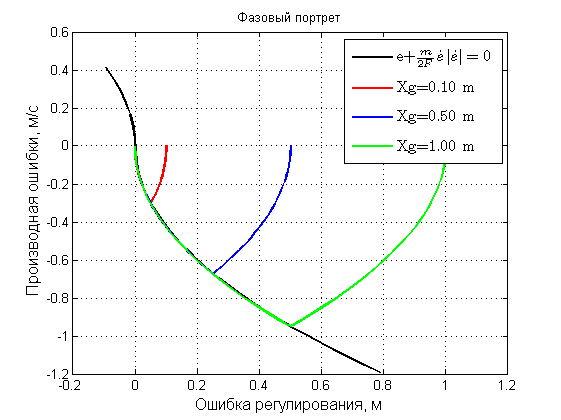
Рисунок 11. Фазовый портрет динамики объекта управления при различных величинах заданного перемещения.

А теперь несколько важных выводов, как того требует правила хорошего тона при проведении экспериментов.

Во-первых MATLAB является исключительно эффективным инструментом в изучении и освоении теории автоматического управления.

Во-вторых, как и следовало ожидать, при различных величинах заданного перемещения поведение системы однозначно соответствует теории релейного оптимального управления. При соответствии расчетных и реальных величин система работает по оптимальному алгоритму и максимально быстро приводит объект управления в заданное положение.

Практический смысл полученных результатов очевиден – для объекта управления со структурой, представленной на рисунке 2, получен ЭТАЛОН переходных процессов. Когда, в дальнейшем, мы будем исследовать различные нюансы систем автоматического управления мы всегда будем иметь пример, как должна вести себя идеальная система управления. Это даст возможность объективно оценить эффективность работы различных алгоритмов управления при наличии расхождений между реальными и расчетными параметрами объекта управления, внешних воздействия на объект управления, дискретизации по времени и по уровню сигналов в системе управления, погрешности измерения и других особенностях физической реализации.

Модель и исходники MATLAB2006

В поисках идеала<< Оглавление >>Где начинается кибернетика

Комментарии (3) на “Берем MATLAB за Simulink. Самая простая модель системы управления”