Лиха беда начало. Самый простой объект управления.

20.03.2010 |

Сначала у меня было желание начать свое повествование с экскурса в теорию линейных систем автоматического управления. Вот я беру учебник, например «» и… Я представляю, как начинает рыдать над этим учебником третьекурсник, например, Военмеха. Сплошные формулы, обобщения, матрицы, модели чего такого и все это, как правило, накануне экзамена.

Конечно, мне очень нравиться эта стройная теория, я ее очень люблю, но не использую. Потому что для простых систем управления эта теория практически бесполезна. Я даже смею утверждать, что ее изучение, без предварительной экспериментальной подготовки вредна для юных неокрепших умов, так как вносит диссонанс между изучаемой теорией и наблюдаемой действительностью . Но это мое личное мнение.

Однако же с чего то начинать надо, поэтому вспоминаем седьмой класс школы по физике с того места, где встречается термин «материальная точка». Второй закон Ньютона как раз про нее. А что бы вспоминалось побыстрей решим следующую задачу - попробуем, например, разработать систему управления для тележки, снабженную приводом, который создает тягу- силу, которая может либо разгонять, либо тормозить тележку.

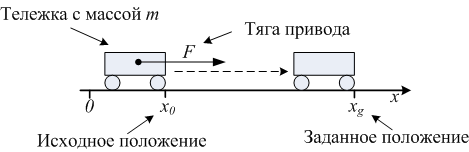
Рисунок 2. Иллюстрация к задаче автоматического управления тележкой

Уточним и формализуем поставленную задачу. И так будем считать, что наша тележка двигается строго по горизонтальной прямой, как это показано на рисунке 2, и ее положение определяется координатой $x$ . Масса $m$ заранее известна. В начальный момент времени тележка находится в исходном положении с координатой $x_0$ . Нам же необходимо, что бы тележка как можно быстро переместилась в положение с координатой $x_g$ . Это положение будем называть “заданным”.

Тяга привода $F$ имеет ограничение, которое обозначим через $F_{max}$ . Тяга привода не может превышать эту величину, независимо от того, в какую сторону она направлена: $-F_{max} \geq F \geq F_{max}$ .

Задачу управления сформулируем следующим образом: необходимо обеспечить такую тягу привода , что бы тележка максимально быстро переместилась из исходного положения $x_0$ в заданное положение $x_g$ .

Тут следует обратить внимание на наиважнейший нюанс («до свидания теория линейного управления») ТЯГА ПРИВОДА ОГРАНИЧЕНА. То есть привод не может толкать нашу тележку, с какой угодно большой силой. Наверно ни кто не будет спорить, что подобного рода ограничение будет справедливо для привода любой природы, будь то электроника, гидравлика, механика или пневматика. И для наномоторов неизвестной мне природы это будет то же справедливо (наверное).

Математическая модель, описывающая физический закон движения нашей тележки, действующие в рамках указанных допущений будет выглядеть следующим образом: $\ddot{x}=\frac{F}{m}$ .

Этот закон называется, как вы наверное уже вспомнили- второй закон Ньютона. Как закон звучит в оригинале я и сам не помню, однако смысл его состоит в том, что ускорение материальной точки пропорционально сумме всех действующих на нее сил и обратно пропорционально массе. Напомню, что две точки над переменной $x$ обозначают вторую производную координаты по времени. Еще эта величина называется «ускорение». В учебнике физики та величина обозначается буквой $a$ . Однако я буду пользоваться обозначением второй производной. Потому что рано или поздно мы перейдем к общему виду и физический смысл координаты $x$ потеряет свое пространственное значение. А вот алгоритмы и идеи останутся практически такими, какими они будут получены для материальной точки.

Если выражение «вторая производная», пока что (или уже), мало о чем вам говорит, то, наверное, лучше остановиться на прочтении этой главы и полистать учебник по алгебре или в каком ни будь интернетовском поисковике наберите «производная для школьников». Лично я рекомендую школьный видеокурс на сайте «http://teachpro.ru». Там же освежите в памяти курс по интегралам, потому что именно через интегралы мы запишем закон движения нашей тележки:

$\dot{x}(t)=\dot{x}_0+\int_{0}^{t}{\ddot{x}(\tau)d\tau}$ ,

$x(t)=x_0+\int_{0}^{t}{\dot{x}(\tau)d\tau}$

Эти формулы показывают, какую величину примут координата и ее производная в момент времени $t$ , если в нулевой момент времени тележка находилась в координате $x_0$ , скорость тележки в нулевой момент времени была равной $\dot{x}_0$ и на нее все это время действовала сила, подчиняющаяся закону $F(t)$ .

Теперь осталось сделать следующий шаг, а именно нарисовать СТРУКТУРНУЮ СХЕМУ, представляющую динамику нашей тележки. Структурная схема реализует принцип «лучше один раз увидеть» и позволяет легко осознать, освоить и запомнить главные особенности физических законов, лежащих в основе движения тележки и системы ее управления.

Принцип построения структурной схемы весьма прост. Каждый блок структурной схемы описывает некоторое преобразование одной величины в другую. Например блок «коэффициент усиления» (Gain, как это показано на рисунке 3 , может описать соотношение силы, действующей на тележку и ее ускорение.

$\ddot{x}=\frac{F}{m}$ $\rightarrow$

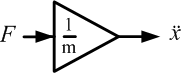Рисунок 3. Элемент структурной схемы- коэффициент усиления.

Мы знаем, что скорость есть интеграл ускорения, на структурной схеме это будет выглядеть так, как показано на рисунке 4.

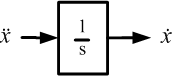$\dot{x}(t)=\dot{x}_0+\int_{0}^{t}{\ddot{x}(\tau)d\tau}$ $\rightarrow$

Рисунок 4. Элемент структурной схемы- интегратор.

Вы наверное обратили внимание, что блок, обозначающий интегрирование входной величины обозначен через ОПЕРАТОР ЛАПЛАСА $s$ . Что бы на данном этапе не усложнять себе жизнь и окончательно не запутаться, воспринимайте этот оператор, как символ, обозначающий дифференцирование по времени, соответственно $\frac{1}{s}$ - интегрирование. Например закон Ньютона, когда масса и сила постоянны, в операторной форме будет выглядеть следующим образом: $s^{2}x=\frac{F}{m}$ , или, что равносильно, : $x=\frac{1}{s^{2}}\frac{F}{m}$ . Отсюда и такое обозначение блока, производящего интегрирование входного сигнала, которое очень часто встречается в литературе и в компьютерных программах, например в MATLAB. Про операторы пока забудем, рано еще. Но при случае про это дело прочитайте – пригодится. Однако в, вернемся к структурной схеме. В целом, структурная схема динамики нашей тележки представлена на рисунке 5.

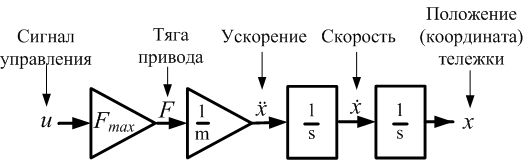
Рисунок 5. Структурная схема динамики тележки.

Обратите внимание, что в структурной схеме появилась еще одна величина , которая называется «сигнал управления». Этот сигнал является безразмерным и изменяется в диапазоне от -1 до 1. Сила, прикладываемая к тележке зависит от этого сигнала следующим образом:

: $F(t)=F_{max}u(t)$ , где $u(t)$ - закон изменения сигнала управления во времени.

Ввел же этот новый сигнал, я только для того, чтобы в дальнейшем было проще перейти к аналогичному управлению объектами произвольной природы.

На этом знакомство с простым объектом управления можно считать состоявшимся и пора приступить к разработке системы автоматического регулирования, о чем пойдет речь в следующей статье, которая так и называется “Из чего состоит система управления“.

Введение<< Оглавление >>Из чего состоит система управления

Рубрика: Новости

LEXA:

24 марта 2010 в 18:39

Я понимаю, что задача написать “ТАУ для чайников” не стояла, но если эта глава начинает погружение в теорию, то она слишком скомканная получилась.
Перечитай Перельмана (Якова Исидоровича) “Занимательная …” (математика, физика и т.д.). Мне нравится его подход: мягко и ненавязчиво вводит читателя в самые научные дебри.

Ответить

admin:

24 марта 2010 в 20:49

Писать для детишек я еще не умею. Многие вещи здесь для меня самоочевидные, со всеми вытекающими:) По честному , я даже не понимаю как навязчиво и мягко рассказать взрослым людям об математической модели тележки.
А на самом деле это материал для третьего курса Военмеха.
Критика есть, жду теперь cоветов;))

Aleksandr:

26 апреля 2011 в 12:44

Здравствуйте!
Занимаюсь программированием климатических камер.
Регулировка температуры и влаги не слишком отличается от управления тележкой, поэтому ваша книга оказалась как нельзя кстати.
Давно хотелось разобраться в пид регуляторах, и написать свой (может даже с автоподстройкой), надеюсь ваша книга мне в этом поможет.

Командор:

19 мая 2011 в 12:55

В скором времени я обязательно напишу про дискретный ПД регулятор. А вот к ПИД регуляторам у меня свой подход, аналогичный адаптивным системам с сигнальной самонастройкой. Об этом тоже скоро напишу

Элементарная теория автоматического управления

Лиха беда начало. Самый простой объект управления.

Комментарии (4) на “Лиха беда начало. Самый простой объект управления.”

Добавить комментарий для Aleksandr